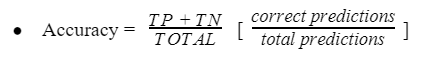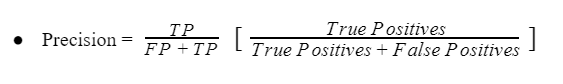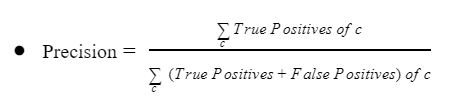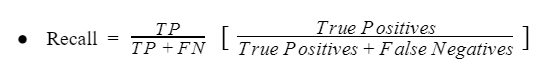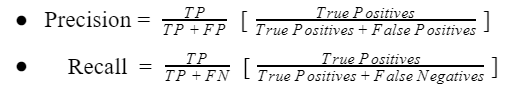
Makine Öğrenmesi Metrikleri - El Kitapçığı
Giriş
Bu el kitabı bir çok kaynak ve şahsi tecrübelerimden de yararlanılarak hazırlanmıştır. Olabildiğince kısa metin içerikleri ile Makine Öğrenmesi Metrikleri ve öğrenme probleminde karşımıza çıkan öğrenememe - aşırı öğrenme (underfitting - overfitting ) konularının açıklanması hedeflenmektedir.
| Model Performansını Arttırmak | Makine Öğrenmesinde Varsayımlar Zinciri |
|---|---|
|
|
Erken Durdurma (Early Stopping) : Birçok insan kendi modelini eğitmek için erken durmayı tercih ediyor. ancak bu durum eğitim verilerinden yeterli verim alınmasını engellemektedir.
Tek Sayı Değerlendirme Metriği
- Confusion Matrix
- Classification Accuracy
- Precision
- Recall
- F-Measure
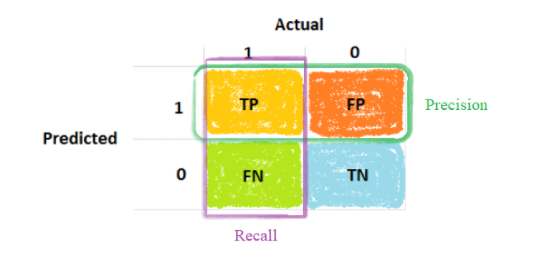
Confusion Matrix
Karışıklık matrisi, bir sınıflandırma problemindeki tahmin sonuçlarının bir özetidir.
Doğru ve yanlış tahminlerin sayısı, sayı değerleriyle özetlenir ve her sınıfa göre ayrılır. Bu, karışıklık matrisinin anahtarıdır.
The confusion matrix shows the ways in which your classification model is confused when it makes predictions.
Confusion Matrix Nasıl Hesaplanır?
Aşağıda bir karışıklık matrisi hesaplama süreci yer almaktadır;
- Beklenen sonuç değerlerine sahip bir test veya doğrulama veri setine ihtiyacınız var.
- Test veri kümenizdeki her satır için tahmin yapın.
- Beklenen sonuçlardan ve tahminlerden:
- Her sınıf için doğru tahmin sayısı.
- Tahmin edilen sınıf tarafından düzenlenen, her sınıf için yanlış tahmin sayısı.
Bu sayılar daha sonra aşağıdaki gibi bir tablo veya matris halinde düzenlenir:
İki Sınıflı Problemler Özeldir
Olay satırını “pozitif”, olaysız satırı ise “negatif” olarak atayabiliriz. Daha sonra tahminlerin olay sütununu “doğru” ve olay olmayanı “yanlış” olarak atayabiliriz.
Bu bize şunları verir;
- Doğru tahmin edilen olay değerleri için “gerçek pozitif - true positive“.
- Yanlış tahmin edilen olay değerleri için “yanlış pozitif - false positive“.
- Doğru tahmin edilen olaysız değerler için “gerçek negatif - true negative“.
- Yanlış tahmin edilen olaysız değerler için “yanlış negatif - false negative“.
Bunu karışıklık matrisinde şu şekilde özetleyebiliriz:
| Gerçek / Tahminlenen | event | no-event |
|---|---|---|
| event | true positive | false positive |
| no-event | false negative | true negative |
Bu, sınıflandırıcımızın precision, recall, specificity ve sensitivity gibi daha gelişmiş sınıflandırma ölçütlerinin hesaplanmasına yardımcı olabilir.
İki Sınıf Uygulaması
>>> import numpy as np
>>> y_true = np.array([1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0])
>>> y_pred = np.array([1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 0, 0])
## Implementation - 1
>>> TN = np.sum(y_pred[y_true == 0] == 0) # 0 - 0 : TN
>>> FP = np.sum(y_pred[y_true == 0] == 1) # 0 - 1 : FN
>>> FN = np.sum(y_pred[y_true == 1] == 0) # 1 - 0 : FP
>>> TP = np.sum(y_pred[y_true == 1] == 1) # 1 - 1 : TP
## Implementation - 2
>>> from sklearn import metrics
>>> confusion_matrix = metrics.confusion_matrix(y_true, y_pred)
>>> tn, fp, fn, tp = confusion_matrix.ravel()
Çoklu Sınıf Uygulaması
## Numeric Implementation
>>> from sklearn.metrics import confusion_matrix
>>> y_true = [2, 0, 2, 2, 0, 1]
>>> y_pred = [0, 0, 2, 2, 0, 2]
>>> confusion_matrix(y_true, y_pred)
array([[2, 0, 0],
[0, 0, 1],
[1, 0, 2]])
## String Implementation
>>> y_true = ["cat", "ant", "cat", "cat", "ant", "bird"]
>>> y_pred = ["ant", "ant", "cat", "cat", "ant", "cat"]
>>> confusion_matrix(y_true, y_pred, labels=["ant", "bird", "cat"])
array([[2, 0, 0],
[0, 0, 1],
[1, 0, 2]])
Classification Accuracy
Sınıflandırma doğruluğu, toplam doğru tahminlerin tahminlerin, tüm tahminlere oranıdır.
Sınıflandırma doğrulu (classification accuracy) uygulamalarda çoğunlukla problemlerle karşılaşmaktadır.
Sınıflandırma doğruluğu ile ilgili temel sorun, sınıflandırma modelinizin performansını daha iyi anlamak için ihtiyaç duyduğunuz ayrıntıyı gizlemesidir. Bu sorunla karşılaşmanızın en olası olduğu iki örnek vardır:
- Verileriniz 2’den fazla sınıfa sahip olduğunda. 3 veya daha fazla sınıfla %80’lik bir sınıflandırma doğruluğu elde edebilirsiniz, ancak bunun tüm sınıfların eşit derecede iyi tahmin edilmesinden mi yoksa model tarafından bir veya iki sınıfın ihmal edilmesinden mi kaynaklandığını bilemezsiniz.
- Verileriniz çift sayıda sınıfa sahip olmadığında. %90 veya daha fazla doğruluk elde edebilirsiniz, ancak her 100 veri için 90 kayıt bir sınıfa aitse bu iyi bir puan değildir ve bu puanı her zaman en yaygın sınıf değerini tahmin ederek elde edebilirsiniz. Örneğin; Kedi, Köpek ve İnsan sınıflandırıcısı geliştirmek istiyorsunuz fakat her 100 veri için elinize 90 adet insan, 5 adet kedi ve 5 adet köpek verisi olduğu varsayıldığında kedi ve köpek için modeliniz sınıflandırma da başarısız, insan ayırt etmede başarılı olduğunu düşünürsek, modelin başarım oranının %90 olacağı öngörülecektir.
Kısaca verinizde dengesiz (unbalanced) veri dağılımı olduğunda sınıflandırma doğruluğu (classification accuracy) metriği bu kusuru sizden saklayacaktır.
Uygulama
>>> from sklearn.metrics import accuracy_score
>>> y_true = [1, 1, 1, 1, 1, 0, 0]
>>> y_pred = [1, 1, 1, 1, 1, 1, 1]
>>> accuracy = accuracy_score(y_true, y_pred)
Precision
Kesinlik (precision), yapılan doğru pozitif tahminlerin sayısını ölçen bir ölçümdür. Bu nedenle Precision, azınlık sınıfı için doğruluğu hesaplar.
Doğru tahmin edilen pozitif örneklerin, tahmin edilen toplam pozitif örnek sayısına oranı olarak hesaplanır.
İkili Sınıflandırma için Precision
İki sınıflı dengesiz bir sınıflandırma probleminde kesinlik, gerçek pozitiflerin sayısının, gerçek pozitiflerin ve yanlış pozitiflerin toplam sayısına bölünmesiyle hesaplanır.
Kesinlik metriğinin sonucu 0.0 (kesinliğin olmadığı) ile 1.0 (kesinliğin olduğu) arasında değer alabilmektedir.
Bu hesabı birkaç örnekle somutlaştıralım.
100 azınlık örneği ve 10.000 çoğunluk sınıfı örneği ile 1:100 azınlık/çoğunluk oranına sahip bir veri kümesi düşünün.
Bir model, azınlık sınıfına ait, 90’ı doğru, 30’u yanlış olmak üzere 120 örnek tahminde bulunur ve tahmin eder.
Bu modelin kesinliği şu şekilde hesaplanır:
- Precision = TruePositives / (TruePositives + FalsePositives)
- Precision = 45 / (45 + 5)
- Precision = 45 / 50
- Precision = 0.90
Bu durumda, model azınlık sınıfına ait olarak çok daha az örnek öngörmesine rağmen, doğru olumlu örneklerin oranı çok daha iyidir.
Bu, hassasiyet değeri faydalı olmasına rağmen, tüm hikayeyi anlatmadığı ortadadır.
Yanlış negatifler olarak adlandırılan negatif sınıfa ait olduğu tahmin edilen gerçek pozitif sınıf örneklerinin sayısı hakkında yorum yapmaz.
Uygulama
###################################################################
# calculates precision for 1:100 dataset with 90 tp and 30 fp
###################################################################
>>> from sklearn.metrics import precision_score
# define actual
>>> act_pos = [1 for _ in range(100)]
>>> act_neg = [0 for _ in range(10000)]
>>> y_true = act_pos + act_neg
# define predictions
>>> pred_pos = [0 for _ in range(10)] + [1 for _ in range(90)]
>>> pred_neg = [1 for _ in range(30)] + [0 for _ in range(9970)]
>>> y_pred = pred_pos + pred_neg
# calculate prediction
>>> precision = precision_score(y_true, y_pred, average='binary')
>>> print('Precision: %.3f' % precision)
Çok Sınıflı Sınıflandırma için Precision
Kesinlik ölçütü ikili sınıflandırma problemleri ile kısıtlı değildir.
Örneğin;
Çoğunluk sınıfının negatif sınıf olduğu bir dengesiz çok sınıflı sınıflandırma problemine sahip olabiliriz.
Bu durumda, pozitif sınıflarımız (sınıf-1 ve sınıf-2 olsun) azınlıkta olacaktır.
Kesinlik, her iki pozitif sınıf arasında doğru tahminlerin oranını ölçebilir.
1:1:100 azınlık/çoğunluk sınıfı oranına sahip, yani her pozitif sınıf için 1:1 oranı ve azınlık sınıfları için çoğunluk sınıfına oranı 1:100 olan bir veri kümesi düşünün ve her azınlıkta 100 her çoğunluk sınıfında 10.000 örneğimiz olsun.
Bir model;
- birinci azınlık sınıfı için 50’sinin doğru ve 20’sinin yanlış olduğu 70 örnek tahminde bulunsun.
- İkinci sınıf için 99 doğru ve 51 yanlış ile 150 tahminde bulunsun.
Bu model için hassasiyet aşağıdaki gibi hesaplanabilir:
- Precision = (TruePositives_1 + TruePositives_2) / ((TruePositives_1 + TruePositives_2) + (FalsePositives_1 + FalsePositives_2) )
- Precision = (50 + 99) / ((50 + 99) + (20 + 51))
- Precision = 149 / (149 + 71)
- Precision = 149 / 220
- Precision = 0.677
Azınlık sınıflarının sayısını artırdıkça hassas metrik hesaplamanın ölçeklendiğini görebiliriz.
Uygulama
###################################################################
# calculates precision for 1:1:100 dataset with 50tp,20fp, 99tp,51fp
###################################################################
>>> from sklearn.metrics import precision_score
# define actual
>>> act_pos1 = [1 for _ in range(100)]
>>> act_pos2 = [2 for _ in range(100)]
>>> act_neg = [0 for _ in range(10000)]
>>> y_true = act_pos1 + act_pos2 + act_neg
# define predictions
>>> pred_pos1 = [0 for _ in range(50)] + [1 for _ in range(50)]
>>> pred_pos2 = [0 for _ in range(1)] + [2 for _ in range(99)]
>>> pred_neg = [1 for _ in range(20)] \
+ [2 for _ in range(51)] \
+ [0 for _ in range(9929)]
>>> y_pred = pred_pos1 + pred_pos2 + pred_neg
# calculate prediction
>>> precision = precision_score(y_true, y_pred, labels=[1,2], average='micro')
>>> print('Precision: %.3f' % precision)
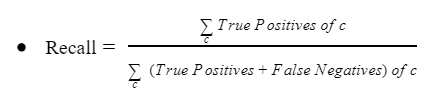
Recall
Duyarlılık (recall), yapılabilecek tüm pozitif tahminlerden yapılan doğru pozitif tahminlerin sayısını ölçen bir ölçümdür.
Tüm pozitif tahminlerden yalnızca doğru pozitif tahminler hakkında yorum yapan kesinliğin aksine, duyarlılık, kaçırılan pozitif tahminlerin bir göstergesini sağlar.
İkili Sınıflandırma için Recall
İki sınıflı dengesiz bir sınıflandırma probleminde, duyarlılık, gerçek pozitiflerin sayısının toplam gerçek pozitif ve yanlış negatif sayısına bölünmesiyle hesaplanır.
Duyarlılık metriğinin sonucu 0.0 (duyarsız) ile 1.0 (tam veya mükemmel duyarlı) arasında değer alabilmektedir.
Bu hesabı birkaç örnekle somutlaştıralım.
Önceki bölümde olduğu gibi, 1:100 azınlık/çoğunluk oranı, 100 azınlık örneği ve 10.000 çoğunluk sınıfı örneği içeren bir veri kümesi düşünün.
Bir model, pozitif sınıf tahminlerinin 90’ını doğru ve 10’unu yanlış tahmin etsin. Bu model için geri çağırmayı aşağıdaki gibi hesaplayabiliriz:
- Recall = TruePositives / (TruePositives + FalseNegatives)
- Recall = 90 / (90 + 10)
- Recall = 90 / 100
- Recall = 0.9
Bu model iyi bir duyarlılığa sahiptir diyebiliriz.
Uygulama
###################################################################
# calculates recall for 1:100 dataset with 90 tp and 10 fn
###################################################################
>>> from sklearn.metrics import recall_score
# define actual
>>> act_pos = [1 for _ in range(100)]
>>> act_neg = [0 for _ in range(10000)]
>>> y_true = act_pos + act_neg
# define predictions
>>> pred_pos = [0 for _ in range(10)] + [1 for _ in range(90)]
>>> pred_neg = [0 for _ in range(10000)]
>>> y_pred = pred_pos + pred_neg
# calculate recall
>>> recall = recall_score(y_true, y_pred, average='binary')
>>> print('Recall: %.3f' % recall)
Çok Sınıflı Sınıflandırma için Recall
Geri çağırma, ikili sınıflandırma problemleriyle sınırlı değildir.
İkiden fazla sınıfı olan bir dengesiz sınıflandırma probleminde, duyarlılık, tüm sınıflardaki doğru pozitiflerin toplamının tüm sınıflardaki doğru pozitiflerin ve yanlış negatiflerin toplamına bölünmesiyle hesaplanır.
Önceki bölümde olduğu gibi, 1:1:100 azınlık/çoğunluk sınıfı oranına, yani her pozitif sınıf için 1:1 oranına ve azınlık sınıfları için çoğunluk sınıfına 1:100 oranına sahip bir veri kümesi düşünün ve her azınlık sınıfında 100 örnek ve çoğunluk sınıfında 10.000 örnek olsun.
Bir model 1. sınıf için 77 örneği doğru, 23 örneği yanlış, 2. sınıf için 95 doğru ve beş örneği yanlış tahmin ediyor.
Bu model için duyarlılığı şu şekilde hesaplayabiliriz:
- Recall = (TruePositives_1 + TruePositives_2) / ((TruePositives_1 + TruePositives_2) + (FalseNegatives_1 + FalseNegatives_2))
- Recall = (77 + 95) / ((77 + 95) + (23 + 5))
- Recall = 172 / (172 + 28)
- Recall = 172 / 200
- Recall = 0.86
Uygulama
###################################################################
# calculates recall for 1:1:100 dataset with 77tp,23fn and 95tp,5fn
###################################################################
>>> from sklearn.metrics import recall_score
# define actual
>>> act_pos1 = [1 for _ in range(100)]
>>> act_pos2 = [2 for _ in range(100)]
>>> act_neg = [0 for _ in range(10000)]
>>> y_true = act_pos1 + act_pos2 + act_neg
# define predictions
>>> pred_pos1 = [0 for _ in range(23)] + [1 for _ in range(77)]
>>> pred_pos2 = [0 for _ in range(5)] + [2 for _ in range(95)]
>>> pred_neg = [0 for _ in range(10000)]
>>> y_pred = pred_pos1 + pred_pos2 + pred_neg
# calculate recall
>>> recall = recall_score(y_true, y_pred, labels=[1,2], average='micro')
>>> print('Recall: %.3f' % recall)
Dengesiz Sınıflandırma Problemlerinde Precision vs. Recall
Dengesiz sınıflandırma probleminizde kesinlik veya duyarlılık metriklerini kullanmaya karar verebilirsiniz.
Bu durumda,
- Kesinliği en üst düzeye çıkarmak, yanlış pozitiflerin sayısını en aza indirirken,
- Duyarlılığı en üst düzeye çıkarmak, yanlış negatiflerin sayısını en aza indirecektir.
Kesinlik: Yanlış pozitifleri en aza indirirken uygun odak noktasıdır. Duyarlılık: Yanlış negatifleri en aza indirirken uygun odak noktasıdır.
Çoğu zaman modelimizden pozitif sınıf için mükemmel tahminler isteriz, yüksek kesinlik ve yüksek duyarlılık.
Özet olarak;
Kesinlik: Mevcut sınıflarımdan kaç tanesini kedi olarak tahmin edebilirim?
Duyarlılık: Kedi olarak kaç tane kedi tahmin edebilirim?
Kesinliğin tanımı, sınıflandırıcınızın kedi olarak tanıdığı örneklerin yüzde kaçı gerçekte kedidir? Dolayısıyla, A sınıflandırıcısı %95 kesinliğe (precision) sahipse, bu, A sınıflandırıcısının bir şeyin kedi olduğunu söylediğinde, bunun gerçekten bir kedi olma ihtimalinin %95 olduğu anlamına gelir.
Duyarlılık, gerçekten kedi olan tüm görüntülerin yüzde kaçı sınıflandırıcınız tarafından doğru olarak tanındı? Peki gerçek kedilerin yüzde kaçı, doğru tanınıyor?
Dolayısıyla, A sınıflandırıcısı %90 duyarlı ise, bu, diyelim ki, geliştirici setlerinizdeki tüm görüntülerin gerçekten kedi olduğu anlamına geliyorsa, sınıflandırıcı A bunların %90’ını doğru bir şekilde tahminleyebildi.
Bu yüzden kesinlik ve duyarlılık tanımları hakkında çok fazla endişelenmeyin. Kesinlik ve duyarlılık arasında genellikle bir denge olduğu ve her ikisinin de önemsendiği ortaya çıkar.
Eğer ki sınıflandırıcı bir şeyin kedi olduğunu söylediğinde, bunun gerçekten bir kedi olma olasılığı yüksektir. Ancak kedi olan tüm görüntülerin büyük bir kısmını gerçekten kedi olarak tahminlemesini de istersiniz. Bu nedenle, sınıflandırıcıları kesinliği ve duyarlılığı açısından değerlendirmeye çalışmak mantıklı olabilir. Değerlendirme ölçütü olarak duyarlılık kullanmanın sorunu, eğer A sınıflandırıcısı burada yaptığı gibi duyarlılıkta daha başarılıysa, B sınıflandırıcısının kesinlikte daha iyi olması, o zaman hangi sınıflandırıcının daha iyi olduğundan emin olamamanızdır.
Dengesiz Sınıflandırma Problemleri için F-Measure
Sınıflandırma doğruluğu, model performansını özetlemek için kullanılan tek bir ölçü olduğu için yaygın olarak kullanılmaktadır. F-Measure, hem kesinliği hem de duyarlılık, her iki özelliği de yakalayan tek bir ölçümde birleştirmenin bir yolunu sunar. Tek başına, ne kesinlik ne de duyarlılık tüm hikayeyi anlatmaz. Korkunç duyarlılık ile mükemmel kesinliğe veya alternatif olarak mükemmel duyarlılık ile korkunç kesinliğe sahip olabiliriz. F-ölçümü, her iki endişeyi de tek bir puanla ifade etmenin bir yolunu sunar. İkili veya çok sınıflı bir sınıflandırma problemi için kesinlik ve duyarlılık hesaplandıktan sonra, bu iki metrik F-Measure hesaplamasında birleştirilebilir.
Geleneksel F-Measure aşağıdaki gibi hesaplanır:
- F-Measure = (2 * Precision * Recall) / (Precision + Recall)
Bu, iki kesrin harmonik ortalamasıdır. Buna bazen F-Skoru veya F1-Skoru denir ve dengesiz sınıflandırma problemlerinde kullanılan en yaygın ölçüm olabilir. Kesinlik ve duyarlılık gibi, zayıf bir F-Measure değeri 0.0’dır ve en iyi veya mükemmel bir F-Measure değeri 1.0’dır.
Örneğin, mükemmel bir kesinlik ve duyarlılık değeri, mükemmel bir F-Measure puanı ile sonuçlanır:
- F-Measure = (2 * Precision * Recall) / (Precision + Recall)
- F-Measure = (2 * 1.0 * 1.0) / (1.0 + 1.0)
- F-Measure = (2 * 1.0) / 2.0
- F-Measure = 1.0
Bir örnekle bu hesabı somutlaştıralım.
100 azınlık örneği ve 10.000 çoğunluk sınıfı örneği ile 1:100 azınlık çoğunluk oranına sahip bir ikili sınıflandırma veri kümesini düşünün.
Pozitif sınıf için 150 örnek öngören, 95’i doğru (gerçek pozitifler), yani beşi kaçırıldı (yanlış negatifler) ve 55’i yanlış (yanlış pozitifler) öngören bir model düşünün.
Kesinliği şu şekilde hesaplayabiliriz:
- Precision = TruePositives / (TruePositives + FalsePositives)
- Precision = 95 / (95 + 55)
- Precision = 0.633
Duyarlılığı şu şekilde hesaplayabiliriz:
- Recall = TruePositives / (TruePositives + FalseNegatives)
- Recall = 95 / (95 + 5)
- Recall = 0.95
Görüldüğü gibi modelin kesinliğinin zayıf olduğunu, ancak mükemmel duyarlığı olduğu gözükmektedir.
Son olarak, F-Measure’ı aşağıdaki gibi hesaplayabiliriz:
- F-Measure = (2 * Precision * Recall) / (Precision + Recall)
- F-Measure = (2 * 0.633 * 0.95) / (0.633 + 0.95)
- F-Measure = (2 * 0.601) / 1.583
- F-Measure = 1.202 / 1.583
- F-Measure = 0.759
İyi duyarlılığın, zayıf kesinliği dengeleyerek, iyi veya makul bir F-ölçü puanı verdiğini görebiliriz.
Uygulama
###################################################################
# calculates f1 for 1:100 dataset with 95tp, 5fn, 55fp
###################################################################
>>> from sklearn.metrics import f1_score
# define actual
>>> act_pos = [1 for _ in range(100)]
>>> act_neg = [0 for _ in range(10000)]
>>> y_true = act_pos + act_neg
# define predictions
>>> pred_pos = [0 for _ in range(5)] + [1 for _ in range(95)]
>>> pred_neg = [1 for _ in range(55)] + [0 for _ in range(9945)]
>>> y_pred = pred_pos + pred_neg
# calculate score
>>> score = f1_score(y_true, y_pred, average='binary')
>>> print('F-Measure: %.3f' % score)
Geliştirme ve Test Kümesini Ayarlama
Sonraki süreçte başarıyı elde edeceğini umduğunuz ve başarılı olmanın önemli olduğunu düşündüğünüz verileri yansıtmak için bir geliştirme seti ve test seti seçin.
Geliştirme ve test setlerinizin aynı dağıtımdan gelmesini sağlamanın bir yolunu bulmanızı tavsiye edin.
Veri Kümesini Bölme
Eğer ki 100, 1000, 10000 örneğe sahipsek;
| Train | Dev | Test |
|---|---|---|
| 0.7 | - | 0.3 |
| 0.6 | 0.2 | 0.2 |
Eğer ki 1 milyondan fazla örneğe sahipsek;
| Train | Dev | Test |
|---|---|---|
| 0.98 | 0.01 | 0.01 |
Avoidable Bias
| Dataset-1 (%) | Dataset-2 (%) | |
|---|---|---|
| Humans (Bayes) | 1 | 7.5 |
| Training Error | 8 | 8 |
| Dev Error | 10 | 10 |
Yukarıdaki tabloda görüldüğü gibi “Dataset-1” üzerinde çalışıyorsak; insan hata oranımız %1, derin öğrenme modelimizin hatası Training-Set’te %8 ve Dev-Set’te %10’dur. Eğitim verileri ile insan hatası arasındaki yanlılık görüldüğü gibi %7’dir. Bu bias değeri uygulama alanına göre kabul edilebilir bir değer değildir.
“Dataset-2” üzerinde çalışıyorsak insan hata oranımız %7, derin öğrenme modelimiz Training-Set’te %8 ve Dev-Set’te %10’dur.
İnsan veri setini %7,5 hata ile değerlendirirken eğittiğimiz yapay sinir ağı modeli %8 hata veriyor. Hatalarımız arasındaki mesafe %0,5. Bu hata değeri tolere edilebilecek bir değerdir.
Kullanılabilir biasımız veri seti-1’de %7, veri seti-2’de %0.5’tir. Ve her iki veri seti için de yanlılık (variance) değerimiz %2’dir.
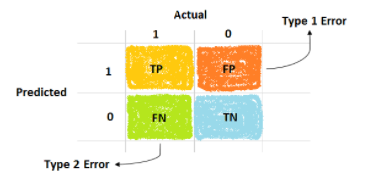
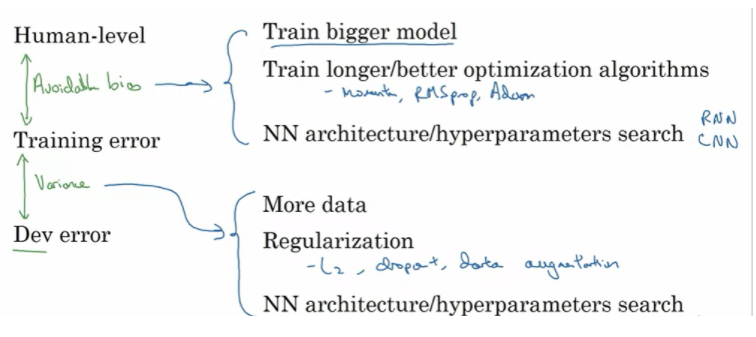
(avoidable) Bias ve Variance Azaltmak
Denetimli Öğrenmenin İki Temel Varsayımı:
- Modeliniz eğitim setinde oldukça iyi performans sağlar. (Kullanılabilir Önyargı)
- Eğitim seti performansı, geliştirme/test setine oldukça iyi genellenir. (Varyans)
Makine öğrenimi sisteminizin performansını artırmak istiyorsanız, eğitim hatanız ile Bayes hatası için proxy’niz arasındaki farka bakılması tavsite edilebilir ve size önlenebilir önyargı hakkında bir fikir verir. Başka bir deyişle, eğitim setinizdeki başarıyı daha iyi ne kadar yapmaya çalışmanız gerektiği hakkında yardımcı olur. Ardından, ne kadar varyans probleminiz olduğuna dair bir tahmin olarak geliştirme hatanız ile eğitim hatası arasındaki farka bakılması gerekmektedir. Başka bir deyişle, performansınızı eğitim setinden açıkça eğitilmediği geliştirici setine genelleştirmek için ne kadar çok çalışmanız gerektiği hakkında bilgi verecektir.
Kaçınılabilir önyargı azaltılmak istendiğinde, daha büyük bir modelde veri setini eğitmek yardımcı olabilir. Böylece, eğitim setlerindeki başarım daha iyi bir hale getirilebilir veya daha uzun süre eğitim gerçekleştirilebilir, ADS momentum veya RMSprop gibi daha iyi bir optimizasyon algoritması kullanabilir veya Adam gibi çok daha iyi bir algoritma tercih edilebilir. Veya denenebilecek başka bir şey, daha iyi bir sinir ağı mimarisi veya daha iyi hiperparametre seti bulmaktır ve bu, aktivasyon fonksiyonunu değiştirmekten, katman veya gizli birimlerin sayısını değiştirmeye kadar her şeyi içerebilir. Bunu yaparsanız, yinelenen sinir ağları ve evrişimli sinir ağları gibi diğer modelleri veya diğer model mimarilerini denemek için model boyutunu artırma yönünde olacaktır. Yeni bir sinir ağı mimarisinin eğitim setinize daha iyi uyup uymayacağını bazen önceden söylemek zordur, ancak bazen daha iyi bir mimari ile çok daha iyi sonuçlar alınabilir. Varyansın bir sorun olduğunu anlamanızın yanı sıra, deneyebileceğiniz birçok teknikten bazıları aşağıdakiler gibidir:
Daha fazla veri elde etmeyi deneyebilirsiniz, çünkü üzerinde eğitmek için daha fazla veri elde etmek, geliştirici küme verilerini daha iyi genelleştirmenize yardımcı olabilir. Düzenlemeyi deneyebilirsiniz. L2 düzenleme, dropout veya veri artırma gibi yöntemler varyansı düzenlemek için yardımcı olabilir veya bir kez daha, bunun bir sinir ağı mimarisi bulmanıza yardımcı olup olmayacağını görmek için çeşitli NN mimarisi/hiperparametre aramasını deneyebilirsiniz probleme daha uygun bir yaklaşım olabilir.
Farklı Dağılımlardaki Veriler için Eğitim ve Test
Müşterilerimiz için telefon ile fotoğrafı çekilmiş nesneler içerisindeki kedileri tespitleyen bir uygulama yapmak isteyelim,
| Websitelerinden Toplanan Veriler | Uygulamamızdan Toplanan Veriler |
|---|---|
| ~200.000 | ~10.000 |
Seçenek - 1
210.000 karıştırılmış veri,
| Shuffled | train | dev | test |
|---|---|---|---|
| Shuffled | 205.000 | 2.500 | 2.500 |
Seçenek - 2
205.000 eğitim kümesi websitesi + uygulamadan toplanan, kalan 5000 dev ve test kümesi için,
| Non-Shuffled | train | dev | test |
|---|---|---|---|
| 205.000 | 2.500 | 2.500 |
Dev ve Test seti dağılımının aynı olmasına özen gösterilmeli.
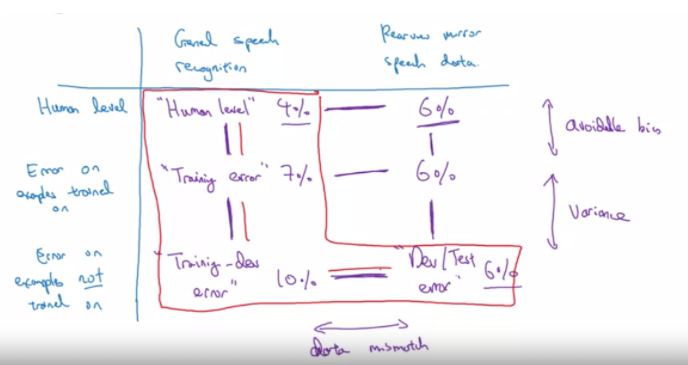
Uyumsuz Veri Dağılımları ile Bias ve Variance
Train set ve Train-Dev set aynı dağılımdan gelmektedir.
Human Error: Veri setinin gözlemci tarafından doğrulanması sonucunda ortaya çıkan hata oranıdır.
Train Error: Modelin, eğitim seti üzerinde gerçekleştirdiği hata oranıdır.
Train-Dev Error: Eğitim seti içerisinden ayıklanmış verinin hata oranıdır.
Dev Error: Eğitim içerisinde model tarafından değerlendirilmeyen verinin hata oranıdır.
| Human Error | 0% |
| Train Error | 1% |
| Train-Dev Error | 9% |
| Dev Error | 10% |
Train Error ile Train-Dev Error arasında %8 hata farkı gözlenmektedir. Bu tablo için variance, overfitting problemi olduğu söylenebilir.
| Human Error | 0% |
| Train Error | 10% |
| Train-Dev Error | 11% |
| Dev Error | 12% |
Human Error ile Train Error arasında %10 hata farkı gözlenmektedir. Bu tablo için bias, underfitting problemi olduğu söylenebilir.
| Human Error | 0% |
| Train Error | 10% |
| Train-Dev Error | 11% |
| Dev Error | 20% |
Human Error ile Train Error arasında %10 hata farkı gözlenmektedir. Öngörülebilir Bias fazla yüksektir.
Train-Dev Error ile Dev Error arasında %9 hata farkı gözlenmektedir. Uyumsuz verinin görülebilir ölçekte yüksek olduğu söylenebilir.
Referans Kaynaklar
-
https://machinelearningmastery.com/confusion-matrix-machine-learning
-
https://machinelearningmastery.com/precision-recall-and-f-measure-for-imbalanced-classification/
-
https://www.veribilimiokulu.com/hata-matrisi-confusion-matrix-python-uygulama/
-
https://scikit-learn.org/stable/modules/generated/sklearn.metrics.confusion_matrix.html
-
DeepLearningAI - Structuring Machine Learning Projects